Neurosymbolic AI: Categories and Case Studies
What and Why is Neuro-symbolic AI?
One of the common sources of confusion when it comes to Neuro-symbolic AI is precisely what it means. This is an understandable confusion because the term itself is extremely broad, and often carries associations that can cause confusion. This isn’t helped with the increasing popularity of neuro-symbolic approaches in fields that come into vogue with the public conciousness, causing laypeople (and the entire marketing department) to use the term in ways that don’t fit with the generally established meaning in literature.
At its core though, the idea is very simple. Neuro-symbolic AI systems describe artificial intelligence systems that combine both neural and symbolic techniques for a single application. Neural techniques, in the context, refer to connectionist approaches to AI, the most prominent being Deep Neural Networks. Symbolic techniques refer to more “traditional” techniques and approaches to AI, these are your chess engines, your reasoning systems, etc. Commonly referred to as rule-based or expert systems, this describes systems where a predefined set of logical rules and mechanisms operates in a deterministic and easily understood way on the problem domain (Bhuyan et al., 2024). Each of these techniques come with their own drawbacks, which quickly became obvious as the fields developed.
Symbolic AI systems were far and away first on the scene, arguably developing even before computers themselves. Of particular interest were applying these techniques to games, since computer scientists have the tendency to also be massive nerds. And their efforts, notably, were met with great initial success. For a small example, take the game of Tic-tac-toe. In the modern day, a novice programmer can create a bot for it using a simple algorithm called Minimax and in so doing create perfect play, such that it will only ever win or draw. This is done by searching through all the moves you could do, and then all the ones your opponent can do, all the way until the end of the game. Then, all you need to do is have the bot choose the moves that are best for it assuming its opponent also played optimally.
This represents a simple example of one of the most powerful early techniques for systems in the field of AI, search algorithms. Other powerful techniques along the same problem domain include reasoning systems, largely based around first-order logic, and knowledge graphs that attempts to represent knowledge as a web of connected nodes.
All these techniques are met with a fundamental problem, however. To make a symbolic system, one needs to understand the problem and then find a way to encode the problem into a computer program. However, in the real world, a lot of the most interesting and difficult problems are also the ones least well-understood. Here, we find salvation in statistics. Statistics reframes the problem, instead of trying to create rules to apply onto the world, it seeks to find trends in the world and predict them, without necessarily needing to understand the trends themselves. Statistics, as described here, includes traditional techniques such as regression and significance tests, but also includes the now powerful subfield of Machine Learning. Machine Learning is simply the application of powerful statistical techniques to attempt to predict trends in often very complex and high-dimensional data.
However, because this data is often very complex, so too do our models become equally complex. As a result, machine learning techniques, especially connectionist approaches based on simulated “neurons”, become virtually inscrutable, with even their own creators unable to fully explain their behavior.
Seeing this, wouldn’t it be nice if we could build systems that incorporated the benefits of both symbolic and neural techniques? This is the goal of Neuro-symbolic AI, however actually combining these two disparate systems proves difficult.
Types of Neuro-symbolic AI
When it comes to actually combining these two techniques many different approaches have been applied. However, these approaches can be categorized into a number of broad trends in application. Notably, these categories are very malleable and a single model can and often do fall into multiple categories. The following is the categorization of Henry Kautz, as presented during AAAI 2020 (Kautz, 2020; Sarker et al., 2021).
Symbolic Neuro Symbolic
Symbolic Neuro Symbolic describes techniques where symbolic operations happen to the inputs and outputs of a network, with the network acting to transform the input into the output before further processing. This describes a whole host of techniques, and in fact most machine learning. Of partiucalar note, this is the cateogization that most LLMs fall into, at least intrinsically, since their inputs and outputs typically have symbolic operations performed on them, with everything from tokenisation, part of speech analysis, and more, not to mention (arguably) attention itself.
Symbolic[Neuro]
Symbolic[Neuro] systems are systems where neural techniques are integrated as subcomponent of an overarching neural technique. This is probably most easily understood by one of the most famous examples, AlphaGo.
AlphaGo
AlphaGo, for those who don’t know already, is a landmark technique for playing the game of Go. Oversimplifying, Go is a game where two players alternately place stones on a board, and stones that are fully surrounded are able to be captured. From a Machine Learning perspective, Go is a difficult game it has a few properties that make it difficult to use search techniques. Namely, it has a high branching factor, that is there are many potential moves for most boards, the games are long, taking many more turns than a game like chess, and winning strategies can be difficult to evaluate, requiring a lot of planning into the future. This leads to computational problems with most search techniques, including advanced ones like Monte-carlo Tree Search (MCTS). AlphaGo solves this by augmenting the MCTS algorithm with deep learning networks in what’s called the policy and value functions, functions that are used by the algorithm to evaluate which moves to search next and how good those moves are likely to be. This allowed the system to perform very well on this problem, and continues to be applied to many games nowadays (Silver et al., 2016).
Neuro[Symbolic]
Neuro[Symbolic] is more-or-less the inverse of Symbolic[Neuro] techniques. Instead of integrating a neural component into a symbolic system, it’s integrating a symbolic component into a system that is otherwise entirely neural. There are many applications for such systems, but an example would be plugins to LLM systems. Concretely, it might be an LLM, a neural system, when told to solve complex math equations, calling Wolfram Alpha, a symbolic system, to help it produce clear and correct mathematical results.
Neuro → Symbolic
Neuro → Symbolic is a pretty straightforward “cascading” system. The result of a neural network is fed into a symbolic system as a whole to produce a final result. This is common in architectures that need to interpret complex input that requires connectionist systems, but look to turn that into a symbolic representation more useful for computers. This is common in natural language processing, as well as many other fields.
Neuro ∪ compile(Symbolic)
Neuro ∪ compile(Symbolic) is the hardest to explain. The idea is to “compile” symbolic rules into a neural network, but not actually constrain the network itself. An example of this would be using a neural network to solve math equations, such as in Lample and Carton, where they use deep learning to solve complex math equations in a way that performs better than symbolic systems (of the time) on some instances (Lample & Charton, 2020).
Trends in Neuro-symbolic Application
There are a variety of different fields where Neuro-symbolic systems are used to great effect. Of particular note are the following.
Explainable AI Systems
Earlier, we discussed one of the disadvantages of Symbolic AI system being the fact that they require a human to be able to understand or model the problem in order to be created. While normally a downside, the flip-side of this is that, typically, symbolic AI systems are much easier for people to understand the final result of such a system. After all, we work with symbolic systems all the time, such as in math, just fine.
However, it should be noted that this isn’t a universal truth. Symbolic systems are typically more explainable but often face issues being difficult to explain at scale. For example, you as a human may be able to intellectually understand what the earlier mentioned mini-max tic-tac-toe algorithm is doing at any given step, but it’s difficult to know exactly what is actually happening with it because of how many branches a game can take. This problem only gets worse in more complex environments, such as in chess, and with more complex techniques, like adding Alpha-Beta pruning or approximations like in Monte-Carlo techniques.
This can be improved by developing ways to visualize symbolic systems, or strip down complex systems into more understandable chunks. A good example of this would be in KG-LLM systems, systems were a symbolic representation of facts, called a Knowledge Graph, is added to a large language model to so that it is able to answer factual questions by drawing on facts from the knowledge base. Obviously, for any non-trivial example, the number of facts a user might ask about is too massive for a human to easily interpret. However, we can visualize just the facts the model queries for a given prompt, and in the process get an idea of where the LLM is getting its information from (and if its getting it from the correct places).
Robustness In Systems
Another area where neuro-symbolic systems do well is systems where a neural solution is required but alone can learn the wrong patterns or be overly fragile. We saw this earlier with KG-LLMs: LLMs are already great on their own at answering queries but they lack an understanding of truth. In their training dataset, there are certainly cases of misinformation, both outright and unintentional. The LLM has no intrinsic way to distinguish truth and lies, and so if we want more robust query answers, such as is required in many domains, it needs to be augmented with a real base of knowledge it can reference.
This links back to the earlier point about explain ability in neuro-symbolic systems. A system that can be explained is going to inherently be more robust for the simple fact that a human can understand more about the process that went into it and is more able to detect mistakes, and it makes it easier to build automated systems to do the same.
Expert Systems
Lastly neuro-symbolic systems are practically required for most expert systems, systems that aims to emulate the decision making of a human expert. This could be, for example, a medical system that aims to give basic first-aid advice in an emergency. Once again, for such systems a level of robustness and explainability in the event of failure (for lawsuits) is required.
Specific Applications
Now that we’ve covered the theoreticals, the what and why, I think the merits of neuro-symbolic systems are best understood by seeing them in their latest real-world use.
Neural Formal Verification (Xie et al., 2022)
The first application we’ll be discussing is a neuro-symbolic system applied to formal verification of neural systems, and building a language to formalize the process.
The broad idea of verification in this context is to ensure that a system will perform as expected, and that for all inputs it gives the expected output. As you’re probably aware, this can be particularly tricky with neural systems because they may learn patterns in the training data that aren’t real patters or reproduce undesirable biases also present in the training set.
Principles and Techniques
First, we should lay some groundwork. After all, formal verification has been around a while and comes in many different forms.
Let’s take a simple example of a system we might want to verify a property of. Let’s say we were constructing a system for determining loan amounts to customers at a bank, and we want to ensure that our fancy new system doesn’t have any overt racial bias.
Another way to put it, we want our system to ensure that the input feature of race has not effect on the output for all examples. This is a fairly simple property that we can now write as a formal equation:
\[x_i \ne x_i' \wedge \bigwedge_{j \ne i} x_j = x_j' \implies f(\overrightarrow{x}) = f(\overrightarrow{x}')\]In this context, $x$ and $x’$ are arrays of all the input features that may or may not correspond to the same input data, indexed by $i$ and $j$, respectively. These serve as input to a neural system, the function $f$. As can be seen, this ensures that for two of the same feature in two different records, identical save for the feature of interest, that the inputs must be identical. In our example, the feature $i$ would be race, and so for any two inputs identical save for the race of the person being evaluated the result should be identical.
Note that this is, intentionally, somewhat of a toy example. for the sake of simplicity, we are intentionally ignoring the complexities of such a system in the real world, such as confounding variables and multicollinearity.
So, now we have something really quite cool! However, we quickly run into issues if we care about properties that are harder to represent in formal notation. To demonstrate this, let’s introduce a new example.
More Complex Examples
Let’s say we’re a cool new company developing a system for a self-driving car, and we think it would be good if we ensured that our car stopped at stop signs. This is something I’ve been told it is good for cars to do.
One thing we might want to ensure in the process might be the statement “whenever a stop sign is in view, the car should be slowing down”. Okay, now how might we write that in formal notation? Instantly we run into a problem because a ton of things in that statement are difficult to concretely define. What is a stop sign? How can I find a stop sign in view?
These kinds of questions are exactly the kinds of ones a neural system is well-suited to solve. So the idea the author build on is, what if we applied a neural network to solve these definitional problems, and then using that network made assertions about the behavior of our larger car network?
To that end, let’s presuppose we have a neural system $g$ that finds when stop signs are in view. Now, it’s trivial to encode our property. For a given set of inputs $\overrightarrow{x}$:
\[g(\overrightarrow{x}) = \text{"yes"} \implies f(\overrightarrow{x}) = \text{"deccelerate"}\]Their Framework
Now that we’ve laid the groundwork, we can talk about the language the authors’ define, called Neuro-symbolic Assertion Language, or NeSEAL. It’s basically the same kinds of things we’ve been writing already, just a little more formal, limited, and explicit.
Formally, the language is a fragment of first-order logic, but removing quantifiers. That is, it’s basically the same logical statements we’ve been making already but the syntax is a little different to be a bit more explicit. Let’s take our example. In NeSEAL, it would be written as:
\[\begin{gather*} \{\overrightarrow{x_1} = \overrightarrow{x_2}\} \\ y_1 \leftarrow f(\overrightarrow{x_1}) \wedge y_2 \leftarrow g(\overrightarrow{x_2}) \\ \{y_2 = \text{yes} \rightarrow y_1 = \text{decelerate}\} \end{gather*}\]You can see that the bones of our same statement are still here. First, we create two input variables $x_1$ and $x_2$, which we then assert are equal. Then, we feed these inputs into two functions: $f$ and $g$. In this context, $f$ is our self-driving car function, and $g$ is the stop sign detecting network. We assign the results to two variables $y_1$ and $y_2$ and ensure that they both succeed with the $\wedge$ clause. Lastly, we assert the property itself, if the $g$ network is currently detecting a stop sign it must imply that the self-driving car is decelerating.
Limitations
So, this is a cool application of neuro-symbolic systems and it’s quite well though-out. However, it does have some practical limitations, with two being immediately obvious to me.
First, it obviously still relies on a neural network being correct, even if it isn’t the same neural network. In this context, if $g$ doesn’t detect a stop sign, the verification can have a false positive and the car might not stop at a stop sign when it really should. However, it should be noted that this is obviously better than the alternative, that being no checks on the system. Ideally, I could see this working quite well if $f$ and $g$ were reasonably independent, such as having different training data and architectures, in the hope that they’d have different failure modes.
Second, it still requires hard-coded properties. This may seem trivial, but for a complex system determining all the validation rules can be very complicated. If you’d like to experience that I recommended trying to formally verify PLC programs it’s very… fun.
Towards Neuro-symbolic Video Understanding (Choi et al., 2025)
Moving on from verification now to computer understanding, let’s talk about one more neuro-symbolic system. Our next system focuses on creating a neuro-symbolic system to better understand videos.
The Problem
To first introduce the problem: let’s say that you’re a user and you want to query an AI system for various information about a video. For a simple example, let’s say you want to find the timestamp in the movie Titanic where the famous “I’m Flying” scene happens.
Simple examples like this can already be done quite well by existing systems that look a video frames and break down their content, which then can be searched. However, this simple approach starts to break down when we start to introduce problems that require a higher degree of temporal understanding. For instance, let’s say we wanted to find the scenes between two major events such as the scenes between the I’m flying scene and the nude drawing scene again the Titanic. This requires a higher degreee of temporal understanding, which many approaches can struggle with.
The authors attribute these difficulties to trying to use a single model for both single-frame features and inter-frame relationships, or more generally spatial and temporal data. To solve this, the authors create a system grounded in temporal logic that are used to query probabilistic automata representing relationships between key frames in the video.
Background
That was a lot of terms to drop, so let’s lay some groundwork before we get into the weeds.
Temporal Logic
First, just what is temporal logic? Temporal logic is a superset of first-order logic that adds additional quantifiers to assert temporal relationships for variables. Now, for the uninitiated, first-order logic is itself a superset of propositional logic, which is just simple statements about variables, this and that must be true, this and that, that kind of thing. First-order logic extends that by adding quantifiers, like this must be true for all instances of this thing, and functions. Temporal logic further extends that by adding even more quantifiers!
To give a few examples:
- Always (◻) - the predicate must always exist temporally
- Eventually/Exist (♦) - the predicate must eventually be true temporally
- Next (X) - two terms must come sequentially, this then that
- Until (U) - similar to next but just to assert that this doesn’t exist until something else exists
For a more complete introduction, feel free to peruse the temporal logic wikipedia page.
Probabilistic Automata Model Checking
Next, I should quickly introduce probabilistic automata. Probabilistic automata are similar to other types of automata you might be familiar with from introductory theoretical computing, such as finite state automata, with the twist being the transition from one state to the next for a given input isn’t deterministic, there’s instead a probability of each potential branch. They’re used in this context due to the uncertain nature of understanding the progression of scenes and events.
For our discussion here, though, one main property is relavent: one can ensure that a probabilistic automata is entailed by a temporal logic statement. This is critical to how queries are built in the system.
Their Solution
With that out of the way, let’s look at a figure from the paper showing an example run by their system.
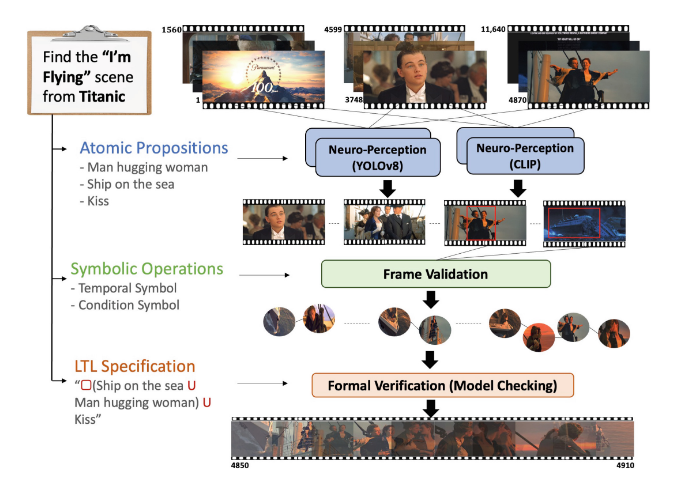
As you can see in the diagram, everything begins with finding the content of a single frame. With their system, this can be done with any off-the-shelf neuro-perception model, in their example they show YOLOv8 and CLIP, which are able to extract wha they call “atomic propositions” from the scene. Things like “man hugging woman” or “ship on the sea”, for a given scene.
These atomic propositions are then fed into the frame validation system, which attempts to extract frames that might be relevant to the prompt, to reduce the search space. It also attempts to assemble the scenes into a probabilistic automata.
Lastly, there’s the stage where this automata is searched for the user’s query. Another network is used to construct a temporal logic specification from the user’s query, and then query can be used to search the automata for where it might be entailed.
Using all this, they were able to build a system more able to query videos with higher accuracy, seeing between a 9 to 15 percent improvement as compared to the SOTA models of the time.
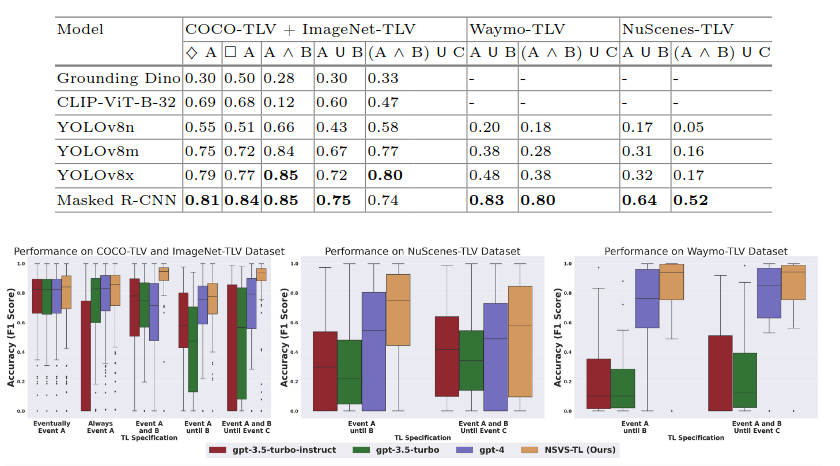
As can be seen in the table, they benchmark their model using a variety of different recognition front-ends and on multiple different datasets and benchmark. They found that a masked R-CNN performs best on most benchmarks with their system. They then compare with state-of-the-art models of the time, namely the GPT models up to GPT-4, since the paper was being written before GPT-4o was released. As can be seen from the box-and-whisker plots, their model performs best on all datasets, by either a narrow or often quite significant margin.
Wrapping Up
These examples show the promise of neuro-symbolic systems, but also some of their pitfalls. They can improve things, but often end up being more complex and hard-to-maintain as a result. Still, they are often a good option and should be considered for an application.
References
- Bhuyan, B. P., Ramdane-Cherif, A., Tomar, R., & Singh, T. P. (2024). Neuro-symbolic artificial intelligence: a survey. Neural Computing and Applications, 36(21), 12809–12844. https://doi.org/10.1007/s00521-024-09960-z
- Kautz, H. A. (2020). The third AI summer: AAAI Robert S. Engelmore Memorial Lecture. AI Magazine, 43(1), 105–125. https://doi.org/https://doi.org/10.1002/aaai.12036
- Sarker, M. K., Zhou, L., Eberhart, A., & Hitzler, P. (2021). Neuro-Symbolic Artificial Intelligence: Current Trends. arXiv. https://doi.org/10.48550/arXiv.2105.05330
- Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., van den Driessche, G., Schrittwieser, J., Antonoglou, I., Panneershelvam, V., Lanctot, M., Dieleman, S., Grewe, D., Nham, J., Kalchbrenner, N., Sutskever, I., Lillicrap, T., Leach, M., Kavukcuoglu, K., Graepel, T., & Hassabis, D. (2016). Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587), 484–489. https://doi.org/10.1038/nature16961
- Lample, G., & Charton, F. (2020). Deep Learning For Symbolic Mathematics. International Conference on Learning Representations. https://openreview.net/forum?id=S1eZYeHFDS
- Xie, X., Kersting, K., & Neider, D. (2022). Neuro-Symbolic Verification of Deep Neural Networks. arXiv. https://doi.org/10.48550/arXiv.2203.00938
- Choi, M., Goel, H., Omama, M., Yang, Y., Shah, S., & Chinchali, S. (2025). Towards Neuro-Symbolic Video Understanding. In A. Leonardis, E. Ricci, S. Roth, O. Russakovsky, T. Sattler, & G. Varol (Eds.), Computer Vision – ECCV 2024 (pp. 220–236). Springer Nature Switzerland. https://doi.org/10.1007/978-3-031-73229-4_13